Overview
One of the biggest hurdles in the current quantum computing technology landscape is the absence of quantum memory, i.e., a mechanism for long-term storage of the state of quantum registers. Without quantum memory, computation must always start from scratch, exacerbating the problem of short coherence time of the NISQ devices. For example, it is often the case that the process of loading the input data to a quantum computer already uses up a significant portion of the time budget, leaving little coherence time for the actual algorithm to process the data.
The challenge of quantum memory is both technical and fundamental. Technically, there is no known way to couple a quantum device to another quantum system and retain its coherence for a long period of time. Even if such a device existed, fundamentally, the quantum no-cloning theorem dictates that the device will not be able to simply copy the quantum state of a quantum computer without destroying the state of the latter. Similarly, the state of the quantum memory would be destroyed once its content is loaded onto a quantum computer, further limiting its usefulness.
Research
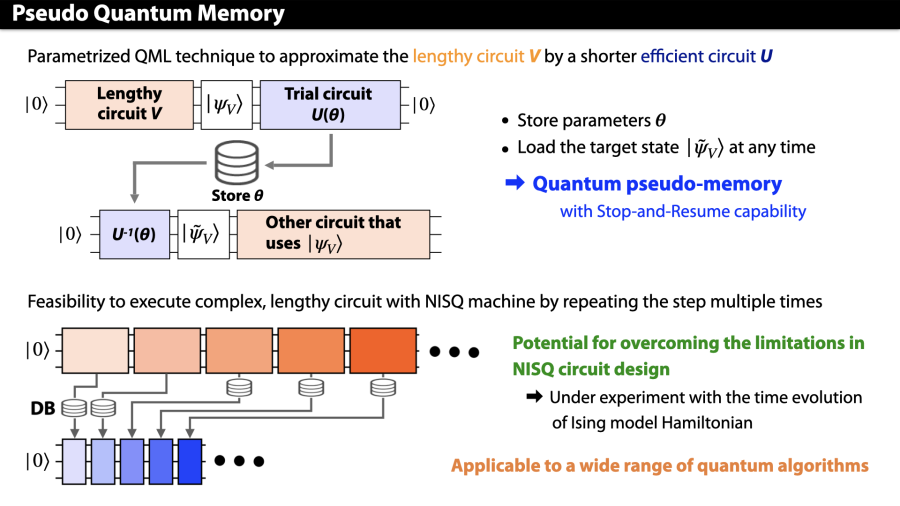
To work around these problems, we are exploring methods to approximately copy and store the state of a quantum computer. Our approach is to utilize a short parametrized quantum circuit to “uncompute” the state (restore the initial state) of a quantum computer at a given point in the quantum circuit. Variational quantum algorithms are employed to find the set of parameter values that minimizes the distance between the uncomputed and initial states. Once the optimal parameters are identified, the inverse of the uncomputing circuit can be used to approximately reconstruct the quantum state created by the original circuit. In this sense, the circuit and the parameter values serve as a form of quantum memory. We are currently refining this method and studying its usability over quantum states created by various algorithms.


 " alt="">
" alt="">