Overview
One of the biggest questions in NISQ applications is whether we can achieve quantum advantage with NISQ devices. Variational Quantum Algorithm (VQA) is expected to be one of the candidates for such applications. In VQA, we first have a parametrized quantum circuit (called ansatz) and measure an observable to obtain a cost function. Then we optimize the cost function with a classical optimizer.
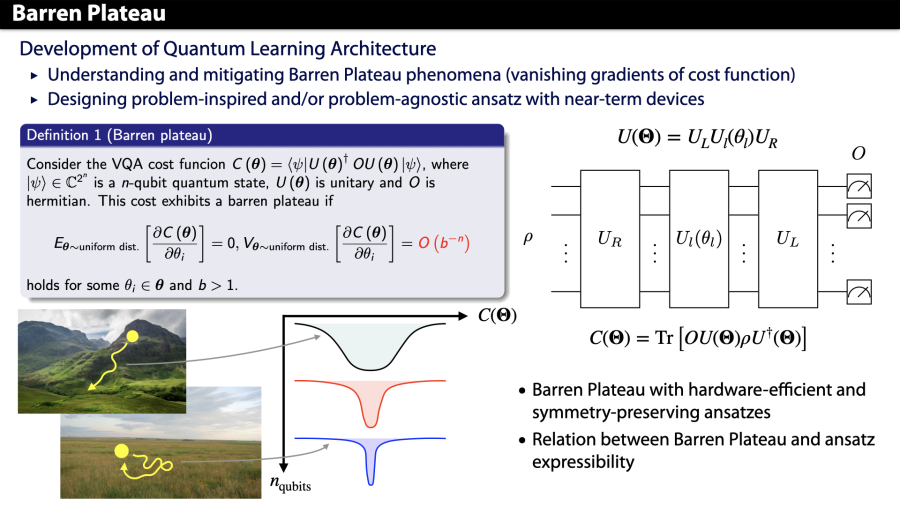
A big problem in this optimization process is a vanishing gradient problem which is the so-called “barren plateau” problem. More precisely, for sufficiently expressive ansatz (i.e., unitary 2-design ansatz), the gradient of a cost function vanishes exponentially when increasing the number of qubits. This is an obstacle to obtaining better scaling over classical algorithms. Furthermore, this problem arises not only in gradient-based optimizers, but also in gradient-free optimizers. Besides, quantum noises can cause similar effects.
We aim to numerically and analytically study effects of barren plateau problems to clarify how and when such problems occur and investigate efficient circuit design to avoid such problems.


 " alt="">
" alt="">